个人训练赛20241211#

C. Diamond Miner
C. MP3
D. Nezzar and Board
E. Hiking

E. Hiking #

Date：Aug.31, 2019 | Rating：2522 | Number of accepted:66(1.53%) | Number of attempts:185(4.30%) | Total:4303

Tag：二分动态规划数论和线性代数

可以涉及的算法：二分 DP 01分数规划

读完题意就可以转化为尽量减少 $\frac{\sum \sqrt{\left| l - r\right |}}{\sum b}$

下面介绍一下01分数规划问题：给定两个都包含 $n$ 个正整数的正数数列{ $a_1,a_2,a_3,...,a_n$ }和{ $b_1,b_2,b_3,...,b_n$ }，同时选出k个a和b，求max $\frac{\sum_{i=1}^{n}a_i s_i }{\sum_{i=1}^{n}b_i s_i }$ ，其中 $s_i=1$ 或 $s_i=0$ 表示选或不选第 $i$ 个数，且 $\sum_{i=1}^{n} s_i=k$ 。

为了加快速度，我们可以用“猜”的方法，猜一个数 $x$ ，使

$\frac{\sum_{i=1}^{n}a_i s_i }{\sum_{i=1}^{n}b_i s_i } \ge x$

移项得 $f = \sum_{i=1}^{n}(a_i - x b_i)\ge k$

01分数规划有两种解决办法：二分法，Dinkelbach算法。

下面利用二分来找到零点：

我们需要最小化一个分式。经典的方法是将分式的最小化问题转化为参数 $\lambda$ 的函数，然后通过二分法寻找最优的 $\lambda$ 。

将原问题转化：

具体来说我们的目标是最小化：

$\frac{\text{总挫败感}}{\text{所用休息点的风景值总和}} = \frac{\sum \sqrt{|l - r_j|}}{\sum b_j}$

设目标函数为：

$\lambda = \frac{\sum \sqrt{|l - r_j|}}{\sum b_j}$

为了最小化这个分式，我们可以令：

$\sum \sqrt{|l - r_j|} - \lambda \sum b_j = 0$

我们可以看成是对于给定的 $\lambda$ ，判断是否存在一条路径，使得：

$\sum \sqrt{|l - r_j|} \leq \lambda \sum b_j$

如果存在这样的路径，我们就尝试更小的 $\lambda$ ；如果不存在，则尝试更大的 $\lambda$ 。

使用二分法寻找最优的 $\lambda$ ：

由于 $\lambda$ 是连续的，我们可以在一个范围内对 $\lambda$ 进行二分搜索，直到找到最小的 $\lambda$ 。

我们可以将休息点看成图中的节点，两个休息点之间的边权为：

$\text{边权} = \sqrt{|l - (x_i - x_j)|} - \lambda b_i$

其中， $x_i$ 是休息点的坐标， $b_i$ 是休息点的风景值。

我们需要找到从起点到终点的最小代价路径，使得总代价 $\leq 0$ 。如果存在这样的路径，那么对于当前的 $\lambda$ ，答案就是可行的。

一些注意点：

实际上思路正确的话，除了二分应该不太会有导致WA的点

二分的判断调节不是hi == lo，因为hi和lo是double，所以要设定一个极小值来进行比较，不然直接比较是有误差的不妨可以试一试下面的代码输出0还是1

1
#include <bits/stdc++.h>
2
using namespace std;
3
int main() {
4
  double a = 0.1, b = 0.2, c = 0.3;
5
  cout << (a + b == c) << endl;
6
}

实际上保留20位小数，a,b,c分别为0.10000000000000000555，0.20000000000000001110，0.29999999999999998890

最后这道题的时间复杂度为 $O(n^{2}log(\sum\sqrt{|l - r_j|}))$

std：

1
#include <bits/stdc++.h>
2
using namespace std;
3
#define int long long
4
using i64 = long long;
5
const int N = 2.01e6;
6
const int M = 1.01e3;
7
const int mod = 998244353;
8
const double eps = 1e-7;
9
#define endl '\n'
10

11
#ifdef LOCAL
12
#include "C:/Users/70510/Desktop/Others/algo/debug.h"
13
#else
14
#define debug(...) 42
15
#endif
16

17
int n;
18
double l;
19
double x[N], b[N];
20
double d[N];
21
int pre[N];
22

23
bool check(double mid) {
24
  for (int i = 0; i <= n; i++) {
25
    d[i] = 1e30;
26
  }
27
  d[0] = 0;
28
  pre[0] = -1;
29
  for (int i = 1; i <= n; i++) {
30
    for (int j = 0; j < i; j++) {
31
      double frustration = sqrt(abs(l - (x[i] - x[j])));
32
      double cost = d[j] + frustration - mid * b[i];
33
      if (d[i] > cost) {
34
        d[i] = cost;
35
        pre[i] = j;
36
      }
37
    }
38
  }
39
  return d[n] <= 0;
40
}
41

42
void solve() {
43
  cin >> n >> l;
44
  for (int i = 1; i <= n; i++) {
45
    cin >> x[i] >> b[i];
46
  }
47
  x[0] = 0;
48
  b[0] = 0;
49
  double lo = 0, hi = 1e6;
50
  while (hi - lo > eps) {
51
    double mid = (lo + hi) / 2;
52
    if (check(mid)) {
53
      hi = mid;
54
    } else {
55
      lo = mid;
56
    }
57
  }
58
  check(hi);
59
  vector<int> ans;
60
  for (int i = n; i != -1; i = pre[i]) {
61
    if (i != 0) {
62
      ans.push_back(i);
63
    }
64
  }
65
  reverse(ans.begin(), ans.end());
66
  for (int i = 0; i < (int)ans.size(); i++) {
67
    cout << ans[i] << " \n"[i == (int)ans.size() - 1];
68
  }
69
}
70

71
signed main() {
72
  ios::sync_with_stdio(false);
73
  cin.tie(0), cout.tie(0);
74
  int T = 1;
75
  // cin >> T;
76
  while (T--) solve();
77
}

01分数规划相关题目：Dropping tests

D. Nezzar and Board #

Date：Jan.28, 2021 | Rating：1972 | Number of accepted:1244(7.68%) | Number of attempts:1672(10.33%) | Total:16192

Tag：构造数学数论

可以涉及的算法：裴蜀定理二元线性丢番图方程

问题描述

给定一个整数序列 $x_1, x_2, \dots, x_n$ ，可以进行以下操作任意次：

选择任意两个整数 $x$ 和 $y$ ，计算 $2x - y$ ，并将结果视为新的整数。

现在，给定一个目标值 $k$ ，问是否可以通过上述操作，从序列中的某个元素出发，经过若干次操作，得到 $k$ 。

为了方便分析，我们先对操作进行等价变换，并理解其本质。

操作等价变换原操作： $2x - y$

可以看作：

$2x - y = x + x - y$ 这样，我们可以将操作视为：从一个元素 $x$ 开始，加上任意两个数的差 $x - y$ 。
由于 $x - y$ 可以为正数或负数，因此，操作的本质是：从某个元素开始，加上任意数对的差。

考虑序列元素之间的差，我们定义序列：

$a_i = x_i - x_{i-1}$ ，对于 $i = 2,3,\dots,n$ 这样，我们可以表示任意两个元素之间的差：
$x_i - x_j = \sum_{k = j+1}^{i} a_k$ ，当 $i > j$ 因此，任意的 $x_i$ 都可以表示为：
$x_i = x_1 + \sum_{k = 2}^{i} a_k$

于是问题转化为：从某个 $x_i$ 出发，通过加上若干个差 $x_p - x_q$ （即 $a$ 的线性组合），得到目标值 $k$ 。

由于差 $x_p - x_q$ 可以表示为 $a$ 的线性组合，且系数为整数（可能为负数），因此，我们可以表示目标值与 $x_i$ 之间的差为： $k - x_i = z_1 a_1 + z_2 a_2 + \dots + z_{n-1} a_{n-1}$ 其中， $z_j$ 为整数。

那么就可以利用裴蜀定理：对于整数序列 $a_1, a_2, \dots, a_{n-1}$ ，存在整数解 $z_1, z_2, \dots, z_{n-1}$ ，使得线性组合等于某个值的充要条件是，该值是这些数的最大公约数 $g$ 的倍数。

因此，我们的问题转化为：是否存在序列中的某个元素 $x_i$ ，使得 $k - x_i$ 是 $g$ 的倍数。

注意到，所有的 $x_i$ 都满足： $x_i \equiv x_1 \pmod{g}$

因为 $x_i - x_1 = \sum_{k=2}^{i} a_k$ ，所以 $x_i - x_1$ 是 $g$ 的倍数。

因此，只需检查 $k$ 是否与 $x_1$ 同余于模 $g$ 意义下，即：如果 $(k - x_1) \mod g = 0$ ，总体时间复杂度 $O(nlog(max(x[i])))$ 。

另外通过丢番图方程入手也可以解决这道题目，手算前几项的递推式可以发现是线性丢番图方程，殊途同归。

科普一个没啥用的小知识：

1
std::__gcd和std::gcd实现并不同，std::__gcd是euclid算法，std::gcd是stein算法，一般来说，随机数据后者效率高，但实际上没人卡这个就是了。

std:

1
#include <bits/stdc++.h>
2
using namespace std;
3
#define int long long
4
using i64 = long long;
5
const int N = 2.01e6;
6
const int M = 1.01e3;
7
const int mod = 998244353;
8
#define endl '\n'
9

10
#ifdef LOCAL
11
#include "C:/Users/70510/Desktop/Others/algo/debug.h"
12
#else
13
#define debug(...) 42
14
#endif
15

16
void solve() {
17
  int n, k;
18
  cin >> n >> k;
19
  vector<int> x(n);
20
  for (int i = 0; i < n; i++) {
21
    cin >> x[i];
22
  }
23
  int g = 0;
24
  for (int i = 1; i < n; i++) {
25
    g = __gcd(g, abs(x[i] - x[i - 1]));
26
  }
27
  int delta = abs(k - x[0]);
28
  if (delta % g == 0) {
29
    cout << "YES" << endl;
30
  } else {
31
    cout << "NO" << endl;
32
  }
33
}
34

35
signed main() {
36
  ios::sync_with_stdio(false);
37
  cin.tie(0), cout.tie(0);
38
  int T = 1;
39
  cin >> T;
40
  while (T--) solve();
41
}

裴蜀定理：【模板】裴蜀定理

裴蜀定理：D. Fox And Jumping

裴蜀定理：Pagodas

裴蜀定理：Function Run Fun

拓展欧几里得算法与二元丢番图方程的解：P1516 青蛙的约会

C. Diamond Miner #

Date：March.10, 2021 | Rating：1176 | Number of accepted:5878(53.86%) | Number of attempts:6593 (60.41%) | Total:10914

Tag：计算几何贪心排序

题意：略

因为坐标每个象限都是等效的，所以我们可以把所有的坐标全都移到同一个想先，为了方便起见，全部都移到第一象限，保证坐标全部为正数，方便计算。

引用官方题解的一张图方便解释：

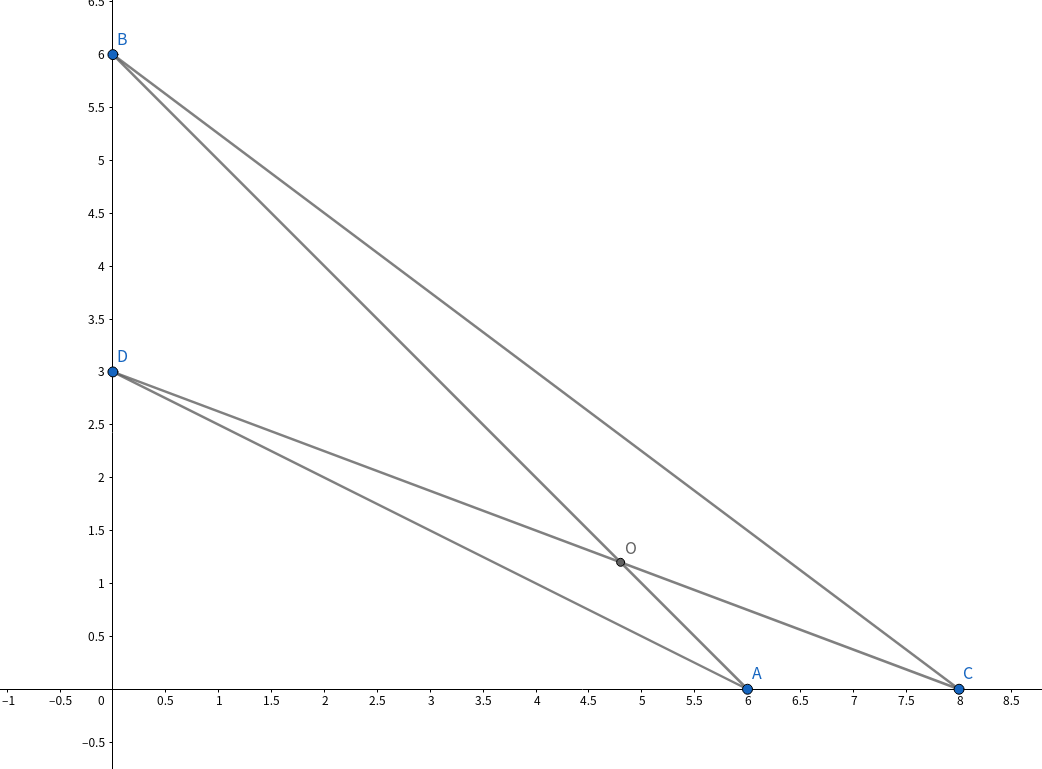
codeforces

我们知道，在三角形中任意两边的长度大于第三遍的长度，在此假设有四个点 $A,B,C,D$ 存在，有两种挖矿的方法

$B$ 挖 $C$ $D$ 挖 $A$ 那么花费的能量为 $|BC|+|AD|$
$B$ 挖 $A$ $D$ 挖 $C$ 那么花费的能量为 $|AB|+|CD|=|AO|+|DO|+|BO|+|CO|>|BC|+|AD|$

显然如果想要花费的能量最小，就是让任意两条线段之间除了定点都不相交

可以将所有的点在 $x$ 轴 $y$ 轴上排序，累加所有的线段就可以得到最小值，时间复杂度为 $O(nlogn)$

std:

1
#include <bits/stdc++.h>
2
using namespace std;
3
#define int long long
4
using i64 = long long;
5
const int N = 2.01e6;
6
const int M = 1.01e3;
7
const int mod = 998244353;
8
#define endl '\n'
9

10
#ifdef LOCAL
11
#include "C:/Users/70510/Desktop/Others/algo/debug.h"
12
#else
13
#define debug(...) 42
14
#endif
15

16
int x[N], y[N];
17

18
void solve() {
19
  int n;
20
  cin >> n;
21
  vector<double> xx;
22
  vector<double> yy;
23
  int totalPoints = n * 2;
24
  for (int i = 0; i < totalPoints; ++i) {
25
    int x, y;
26
    cin >> x >> y;
27
    if (x == 0) {
28
      yy.push_back(abs(y));
29
    } else if (y == 0) {
30
      xx.push_back(abs(x));
31
    }
32
  }
33
  sort(yy.begin(), yy.end());
34
  sort(xx.begin(), xx.end());
35
  double ans = 0.0;
36
  for (int i = 0; i < n; ++i) {
37
    double dis = sqrt(yy[i] * yy[i] + xx[i] * xx[i]);
38
    ans += dis;
39
  }
40
  cout << fixed << setprecision(15) << ans << endl;
41
}
42

43
signed main() {
44
  ios::sync_with_stdio(false);
45
  cin.tie(0), cout.tie(0);
46
  int T = 1;
47
  cin >> T;
48
  while (T--) solve();
49
}

C. MP3 #

Date：July 30, 2019 | Rating：1748 | Number of accepted:1884(26.85%) | Number of attempts:4402(62.74%) | Total:7016

Tag：双指针

题意：略

首先，我们需要计算在给定磁盘大小下，数组中最多可以有多少个不同的值。

每个值需要的位数为 $k = \lceil \log_2 K \rceil$ ，总共需要的位数为 $n \times k$ 。磁盘大小为 $I$ 字节，即 $8I$ 位。

因此，需要满足： $n \times k \leq 8I$ ，即： $k \leq \dfrac{8I}{n}$ ，由于 $k$ 为非负整数，我们取其下界。

然后，不同值的最大数量 $K$ 满足： $K \leq 2^k$ ，由于 $k = \lceil \log_2 K \rceil$ ，所以： $K \leq 2^{\frac{8I}{n}}$

但是， $K$ 最多为 $n$ ，因为数组长度为 $n$ 。

为了避免 $K$ 过大（当 $n$ 很小时， $2^{\frac{8I}{n}}$ 可能很大），我们可以设定一个上限，比如 $K_{\text{max}} = n$ 。

我们可以对数组进行预处理：排序+统计数组中不同元素的值及其出现次数，进而滑动窗口寻找最优区间

我们的目标是：

选择一个包含不超过 $K$ 个不同值的子区间（这些值是连续的，因为经过排序）；
使得在这个区间内的元素数量尽可能多，从而被修改的元素数量尽可能少；

具体来讲：

设定一个滑动窗口，初始化左端点和右端点；
枚举所有可能的左右端点组合，使得窗口内的不同值数量不超过 $K$ ；
计算每种情况下需要修改的元素数量，即总元素数减去窗口内的元素数量；
取需要修改元素数量最小的方案；

总时间复杂度为 $O(n \log n)$ 。

std:

1
#include <bits/stdc++.h>
2
using namespace std;
3
#define int long long
4
using i64 = long long;
5
const int N = 2.01e6;
6
const int M = 1.01e3;
7
const int mod = 998244353;
8
#define endl '\n'
9

10
#ifdef LOCAL
11
#include "C:/Users/70510/Desktop/Others/algo/debug.h"
12
#else
13
#define debug(...) 42
14
#endif
15

16
void solve() {
17
  int n, I;
18
  cin >> n >> I;
19
  vector<int> a(n);
20
  for (int i = 0; i < n; ++i) {
21
    cin >> a[i];
22
  }
23
  sort(a.begin(), a.end());
24
  vector<int> val;
25
  vector<int> count;
26
  vector<int> pre(1, 0);
27
  int cnt = 1;
28
  for (int i = 1; i <= n; ++i) {
29
    if (i == n || a[i] != a[i - 1]) {
30
      val.push_back(a[i - 1]);
31
      count.push_back(cnt);
32
      pre.push_back(pre.back() + cnt);
33
      cnt = 1;
34
    } else {
35
      cnt++;
36
    }
37
  }
38
  int max_bits = (8 * I) / n;
39
  int K;
40
  if (max_bits >= 20) {
41
    K = val.size();
42
  } else {
43
    K = min((int)val.size(), 1LL << max_bits);
44
  }
45
  int cht = n;
46
  int tot_val = val.size();
47
  for (int lo = 0, hi = 0; hi < tot_val; hi++) {
48
    while (hi - lo + 1 > K) {
49
      lo++;
50
    }
51
    int unchanged = pre[hi + 1] - pre[lo];
52
    int changes = n - unchanged;
53
    cht = min(cht, changes);
54
  }
55
  cout << cht << endl;
56
}
57

58
signed main() {
59
  ios::sync_with_stdio(false);
60
  cin.tie(0), cout.tie(0);
61
  int T = 1;
62
  // cin >> T;
63
  while (T--) solve();
64
}

个人训练赛20241211#

E. Hiking#

D. Nezzar and Board#

C. Diamond Miner#

C. MP3#

E. Hiking #

D. Nezzar and Board #

C. Diamond Miner #

C. MP3 #